バイト列のまま大小比較可能な浮動小数点数表現を作った話

この記事はKLab Engineer Advent Calendar 2020の9日目の記事です。

はじめに

オンライン対戦では、レベルや総合力が近いプレイヤー同士をマッチングさせたいという要件がよくあります。マッチングサーバでは、送られてきたプレイヤーのプロパティの値をサーバ側で比較してマッチングさせるか決定します。どのようなプロパティにどのような型の値が入っているかはプロジェクトによって様々です。

クライアントからネットワーク越しに数値を送るためには、何らかの方法でバイト列にシリアライズする必要があります。送られた数値同士をサーバ側で比較するとき、普通ならデシリアライズして元の数値の型に戻してから比較しますが、送られたバイト列のまま比較できたら実装もシンプルになりパフォーマンスも有利になると思われます。

符号なし整数であれば、ビッグエンディアンならバイト列のまま先頭から比較するだけで大小関係がわかります。また、符号付き整数の場合は下駄履き表現(エクセスN)にすることで、バイト列のまま比較可能になります。では浮動小数点数の場合はどうしたらよいでしょう。

IEEE754と大小比較

浮動小数点数は多くの環境でIEEE754のビット列として表現されています。詳しい解説はWikipediaに譲るとして、ここではその大小関係について考えます。

単精度浮動小数のビット列(出典：Wikipedia)

正の数の大小関係

正の数と負の数に分けて考えます。まずは正の数の場合です。

符号ビットは常に0で一定なので大小関係に影響はありません。次に指数部は、最大値のときInf（無限大）とNaN（非数）、最小値のとき0値と非正規化数の浮動小数点数になります。それ以外の中間値のときは正規化数で、指数の下駄ばき表現（エクセスN）になっています。

指数部が最大値のときは、NaNを無視すればInfだけなので、指数部が小さい他の数値より大きいと判断できます。

正規化数はケチ表現なので、指数部をEとすると、浮動小数点数値は1.xxxx… * 2の(E-N)乗です。したがって、Eの値が大きいほうが数値としても大きくなります。指数部が同じ場合、小数点以下をそのまま表している仮数部が大きいほうが大きな数値になります。

最後に指数部が0の非正規化数と0値は、浮動小数点数値は0.xxxx… * 2の(1-N)乗なので、正規化数の最小値（1.xxxx… * 2の(1-N)乗）より小さく、正規化数と同じく仮数部が大きい方が大きな数値になっています。

これらの性質と、指数部が仮数部より上位ビットに配置されることから、IEEE754で表現されたビット列と浮動小数点数値では大小関係が一致していることがわかります。

負の数の大小関係

続いて負の数の場合をみていきます。先程示した正の数と異なり、負の数では符号を除いた値（絶対値）が大きいほど数値としては小さくなります。つまり、ビット列と浮動小数点数値では大小関係が真逆になってしまっています。

バイト列のまま大小比較可能な表現

ここまで、IEEE754のビット列と浮動小数点数値の大小関係について整理しました。ではこのビット表現をちょっとだけ加工して、まずはビット列のまま大小比較出来るようにしてみます（ただしNaNは無視します）。

最上位の符号ビットは、正の数が0で負の数が1でした。これを反転させてあげると、ビット列として正の数が負の数より必ず大きくなります。

正の数の場合、残りのビット列と浮動小数点数値はすでに大小関係が一致していました。一方負の数では大小関係が真逆だったので、負の数のときだけ全ビットを反転することで順序を逆転してあげます。

整理すると、正の数は符号ビットのみ反転、負の数は符号ビット含めすべて反転することで、ビット列と浮動小数点数値の大小関係を一致させることができます（+0 > -0となってしまうのはご愛嬌）。これをビッグエンディアンでバイト列にすれば、バイト列のまま先頭から比較していくことで大小比較可能になります。

戻すときは逆の変換をするだけです。最上位ビットが1のときは最上位ビットのみを、0のときは全ビットを反転させてから、IEEE754として浮動小数点数に変換すれば元に戻ります。

実装とパフォーマンス

Go言語で倍精度浮動小数の変換を実装すると次のようになります。

func ToComparable(b []byte, f float64) {
	v := math.Float64bits(f)
	if v&(1<<63) == 0 {
		v ^= 1 << 63
	} else {
		v = ^v
	}
	binary.BigEndian.PutUint64(b, v)
}

func FromComparable(b []byte) float64 {
	v := binary.BigEndian.Uint64(b)
	if v&(1<<63) != 0 {
		v ^= 1 << 63
	} else {
		v = ^v
	}
	return math.Float64frombits(v)
}

パフォーマンス

(12/9 14時ころ修正：ベンチマークのとり方を勘違いしていました。おりさのさんありがとうございます）

テストとベンチマークのコードをGo Playgroundに置いておきました。 https://play.golang.org/p/j0hUgVfqfCe

変換した値を元に戻せるかと、大小関係を正しく判定できるかのテストを、Playground上で実行できます。

また、このコードをmain_test.goとして保存し、手元の環境でのベンチマークを走らせてみました。（実行環境：Kubuntu 20.04、Intel Core i7-6700、go version go1.15.5 linux/amd64）

makki@home:~/test/compfloat$ go test -bench=. -count=5
goos: linux
goarch: amd64
pkg: main/compfloat
BenchmarkCompIEEE754-8                     16392             70919 ns/op
BenchmarkCompIEEE754-8                     16657             71587 ns/op
BenchmarkCompIEEE754-8                     16716             70880 ns/op
BenchmarkCompIEEE754-8                     16734             70683 ns/op
BenchmarkCompIEEE754-8                     16660             71165 ns/op
BenchmarkNoInlineIEEE754-8                 17214             70974 ns/op
BenchmarkNoInlineIEEE754-8                 17289             71064 ns/op
BenchmarkNoInlineIEEE754-8                 17312             70658 ns/op
BenchmarkNoInlineIEEE754-8                 17163             70416 ns/op
BenchmarkNoInlineIEEE754-8                 17072             70185 ns/op
BenchmarkCompComparable-8                  26832             42408 ns/op
BenchmarkCompComparable-8                  28588             43257 ns/op
BenchmarkCompComparable-8                  28620             42407 ns/op
BenchmarkCompComparable-8                  26536             42542 ns/op
BenchmarkCompComparable-8                  28347             43043 ns/op
BenchmarkNoInlineComparable-8              18874             64007 ns/op
BenchmarkNoInlineComparable-8              18582             63699 ns/op
BenchmarkNoInlineComparable-8              18578             63670 ns/op
BenchmarkNoInlineComparable-8              18460             63858 ns/op
BenchmarkNoInlineComparable-8              18883             64681 ns/op
PASS
ok      main/compfloat  36.554s

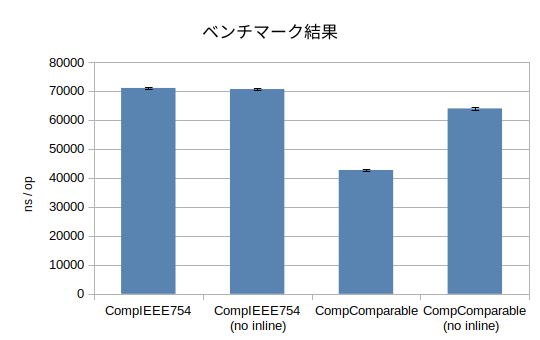
ベンチマーク結果

バイト列のまま比較したCompComparableは、内部でbytes.Compareを呼ぶだけなのでコンパイル時にインライン展開されるようです。その結果、float64に戻して比較するCompIEEE754にくらべて約6割程度の処理時間になっています。またインライン展開を抑制した場合でも、1割程度高速化できています。（元の処理が小さいので、関数呼び出しオーバーヘッドの割合が大きいですね。）

まとめ

バイト列のまま大小比較可能な浮動小数点数のビット表現を作りました。そしてバイト列のままの比較する方が、浮動小数点数にデシリアライズして比較するより高速なことも示しました。

バイト列のままの比較はベンチマークのコードでも示したとおり、Go言語では標準パッケージのbytes.Compareでできます。また、浮動小数点数同士だけなく他の整数型同士の場合も、下駄履き表現のビッグエンディアンとすることでバイト列のまま比較できるので、サーバ側でのプロパティ値の比較は、型による分岐が不要なシンプルな実装にすることができます（もちろん型が一致しないと比較はできません）。

以上、大規模なオンライン対戦ゲームを支えるためのちょっとした工夫の紹介でした。